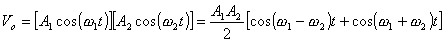 (1)
(1)| More Tutorials |
Introduction to Mixers
Michael Ellis, All Rights Reserved, 1999
Mixers are used for frequency conversion and are critical components in modern radio frequency (RF) systems. A mixer converts RF power at one frequency into power at another frequency to make signal processing easier and also inexpensive. A fundamental reason for frequency conversion is to allow amplification of the received signal at a frequency other than the RF, or the audio, frequency. A receiver may require as much as 140 decibels (dB) of gain. It might not be possible to put more than 40 dB of gain into the RF section without risking instability and potential oscillations. Likewise the gain of the audio section might be limited to 60 dB because of parasitic feedback paths, and microphonics. The additional gain needed for a sensitive receiver is normally achieved in an intermediate frequency (IF) section of the receiver
The ideal mixer, represented by figure 1, is a device which multiplies two input signals. If the inputs are sinusoids, the ideal mixer output is the sum and difference frequencies given by
 (1)
(1)
Typically, either the sum, or the difference, frequency is removed with a filter.
Figure 2 shows the front end for an amplitude modulation (AM) superheterodyne radio with a tuned RF section that allows only the preselected RF frequency to the input of the mixer. Figure 3 improves the front end image rejection by adding an additional tuned RF circuit. Assuming the desired station is transmitting at 1490 KHz, with a high side local oscillator (LO) of 1945 KHz, and an IF of 455 KHz, then a station transmitting at 2400 KHz would also convert to an IF of 455 KHz, interfering with the desired station, if the 2400 KHz signal were not filtered out prior to the mixer input. In a typical AM radio, the front end is tuned simultaneously with the LO at a constant difference of 455 KHz over the entire AM radio band of 550 - 1600 KHz.
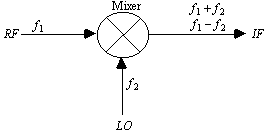
Figure 1. Circuit symbol for a mixer
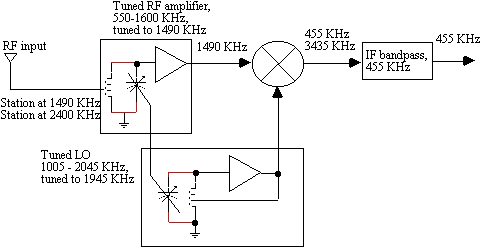
Figure 2. Superheterodyne radio front end
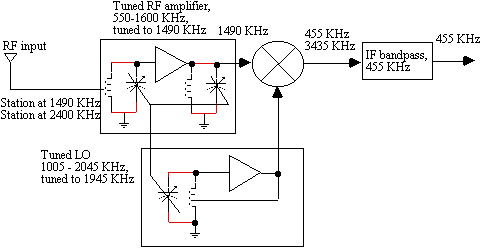
Figure 3. Superheterodyne AM radio front end with improved front end filtering
This requires a specially constructed dual ganged-variable capacitor to tune both sections simultaneously and retain a constant 455 KHz difference. Typically the LO section of the ganged-variable capacitor will have fewer plates than the RF amplifier section. This type of ganged-variable capacitor is called the cut-plate capacitor because the LO section plates are cut to permit tracking of the LO with the RF. The undesired frequency of 2400 KHz is called the image frequency and must be eliminated prior to conversion. The 455 KHz IF filter eliminates the sum frequency of 3435 KHz which contains redundant information.
FM radios, which tune over 88 - 108 MHz, usually do not use a 455 KHz IF frequency since the image frequency would be only 910 KHz from the desired FM station. It would be difficult to design a tuned RF amplifier in the 88 - 108 MHz range that rejected a station only 910 KHz away from the desired signal since 910 KHz is only about 1% different in frequency than the desired FM station. An IF of 10.7 MHz is normally used in FM radios to allow adequate image rejection to be achieved by the tuned RF amplifier in the 88 - 108 MHz band with reduced selectivity because of the higher IF bandwidth associated with a 10.7 MHz IF filter. The double conversion receiver of figure 4 is appropriate for VHF narrowband AM or FM operation and uses a 10.7 MHz 1st IF for good image rejection, and a 455 KHz 2nd IF for good selectivity.
The double conversion receiver in figure 5 does not require a tunable RF stage to track the tunable LO because the first IF of 830 MHz causes the image frequencies to be outside the bandpass of the 0-30 MHz input filter. This technique of commonly used in communication grade receivers, CATV tuners, and spectrum analyzers.
The direct conversion receiver of figure 6 suffers from several disadvantages. It does not have an intermediate frequency (IF) stage. The purpose of an IF stage is to allow additional amplification at an non-harmonically related frequency that will not feed back into the RF input and cause oscillation. The gain of the direction conversion receiver is therefore limited to the gain of any RF amplifiers preceding the mixer, and any audio amplifiers following the mixer. AM and SSB can be demodulated, but not FM. There is usually significant LO feedthrough at the desired frequency which can cause undesired beats in the audio output for AM signals.
In reality, mixers produce more than just the sum and difference frequencies. The intermodulation products are given by IF = N*RF ± M*LO and their levels, relative to the desired output of RF ± LO, for a common mixer, are shown in table 1.
In table 1, the spurious outputs are relative to the desired output at RF ± LO. The first harmonic of the RF input signal feeds through to the output and is only 23 dB down from the desired output frequency. The
first harmonic of the LO feeds through at only 1 dB down. The second harmonic of the RF input, mixed with the first harmonic of the LO (2RF ± LO), feeds through at an amplitude of 59 dB down from the desired output,
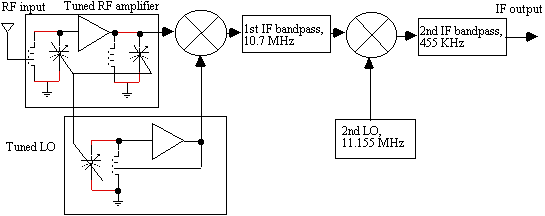
Figure 4. Double conversion superheterodyne with good image rejection and selectivity
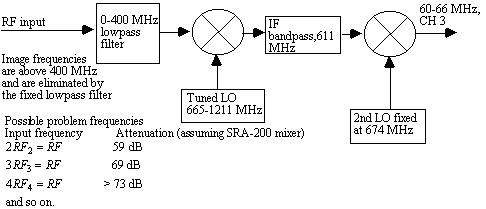
Figure 5. Double conversion receiver in a Scientific-Atlanta series 6700 cable converter box that eliminates the need for simultaneously tuned RF and LO
and so on. The data given in a harmonic intermodulation table depends on the relative levels of the input signals, the frequencies, and the terminating impedances. From table 1, notice that the SRA-200 mixer is a poor choice for the direct conversion receiver since the LO leakage is high. Also notice that the front end of the receiver in figure 6 is not tuned, and will also have some response to other RF frequencies as shown in table 1 where 2 RF2 + LO, 3 RF3 + LO, etc., are equal in frequency to the desired signal at frequency RF + LO.
Figure 7 shows a diode ring double-balanced mixer which is usually designed with Schottky barrier diodes. GaAs diodes are sometimes used for operation in the millimeter-wave frequency range. Mixers can also use bipolar transistors, J-FETS, and GaAs FETs, all of which require a fourth port for a dc voltage.
For downconverters the RF input signal is fed to the RF port and the output is taken from the IF port. For upconverting applications using the diode ring double-balanced mixer, the low frequency signal can be fed into the IF port and the output can be taken from the RF port.
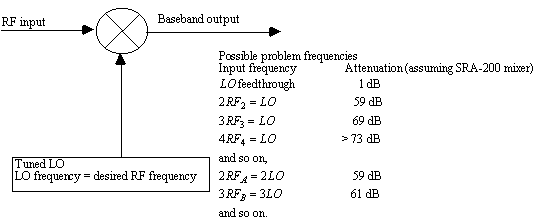
Figure 6. Direct conversion receiver
Table 1
Mixer Harmonic Intermodulation for Mini-Circuits SRA-220, 0.05 - 2000 MHz mixer

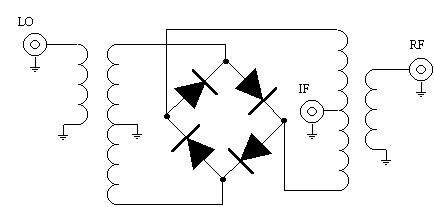
Figure 7. Diode ring double-balanced mixer
Definitions
Conversion Loss is the ratio of the output signal level to the input signal level expressed in dB. In a single sideband system, only one sideband is used; therefore 3 dB of loss is theoretical. The additional loss is diode and transformer loss. These losses can be minimized by driving the diodes with sufficient current and operating in the best portions of the frequency band and are generally between 5 - 9 dB for passive mixers. Conversion loss is specified in a 50 Ω system with an LO drive level of +7 dBm. High level mixers are specified with more LO drive power.
Isolation is the amount of "leakage" or "feedthrough" between the mixer ports. From table 1 for the SRA-220 mixer, the isolation between the LO port and the IF (output) port is only 1 dB, for the test conditions given. At low frequencies, where diode parameters can be matched to a much greater degree and circuit parasitics are negligible, isolation greater than 60 dB is possible.
Noise Figure is the signal-to-noise ratio at the input divided by the signal-to-noise ratio at the output expressed in dB. It does not include the noise figure of an IF amplifier or 1/f flicker noise. Appreciable noise contribution from 1/f noise is not noticeable above 10 KHz. Use of specially selected Schottky-Barrier diodes ensures extremely low 1/f noise for phase detection applications. With the recommended drive level, the noise figure and conversion loss are essentially identical.
The Friis noise figure equation for cascaded devices is given as
![]()
where F is the total noise factor. All terms are numeric ratios and are not in dB. The overall noise figure for a cascade, expressed in dB is
![]()
If a manufacturer of a RF preamplifier specifies that the RF preamp has a 2 dB noise figure, this means that the actual noise power at the output is 1.58 (F = 1.58) times that which would occur due to amplification of the thermal noise from the input. If a device is passive and lossy then the noise figure of that device is generally taken to be the same as its loss. If other words, if a transmission line has a 3 dB loss, it has a noise figure of 3 dB.
Conversion Compression is the RF input level above which the RF versus IF output curve deviates from linearity. Above this level, additional increases in the RF input level do not result in equal increases in the output level. Conversion compression is not specified for all low level (+7 dBm LO) mixers. However, low level mixers normally have the same compression level, typically 0.3 dB deviation from linearity with an RF input signal of +2 dBm and a +7 dBm LO drive level. This RF level can be raised to +4 dBm if the drive level is increased to +13 dBm. Conversion compression for high level mixers is specified since it sometimes provides an indication of the mixer's two tone performance and it is likely to be important in high level operation. The input power level at which the conversion loss increases by 1 dB is called the 1 dB compression point.
Dynamic Range is the amplitude range over which a mixer can operate without degradation of performance. It is bounded by the conversion compression point for high input signals, and by the noise figure of the mixer for low level input signals. Since the thermal noise of each passive mixer is about the same, the conversion compression point normally determines the passive mixer's dynamic range. The 1 dB compression point is generally taken to be the top of the dynamic range of a mixer because the input RF power that is not converted into desired IF output power is instead converted into heat and higher order intermodulation products. The intermodulation products that begin to appear when RF power is increased beyond the 1 dB compression point can begin to obscure the desired IF output. Generally the 1 dB compression point is 5 to 10 dB lower than the LO power, so a high level mixer has a higher 1 dB compression point than a low level mixer, and therefore a wider dynamic range.
Intercept Point, measured in dBm, is a figure of merit for intermodulation product suppression. A high intercept point is desirable. Two types are commonly specified: input ;and output intercept point (IIP and OIP, respectively). Input intercept point is the level of input RF power at which the output power levels of the undesired intermodulation products and IF products would be equal; that is, intercept each other if the mixer did not compress. As input RF power increases, the mixer compresses before the power level of the intermodulation products can increase to equal the IF output p;ower. So, input and output intercept points are theoretical and are calculated by extrapolating teh output power of the intermodulation and IF products past the 1-dB compression point until they equal each other. A high intercept point is desirable because it means the mixer can handle more input RF power before causing undesired productgs to rival the desired IF output product, and essentially means the mixer has a greater dynamic range. Dynamic range, 1-dB compression point, and intercept point are all interrelated, but it has been shown that, in general, no dB-for -dB rule of thumb exists to easily correlate 1-dB compression point with intercept point.
The concept of intercept point can be applied to any intermodulation product; however, it normally refers to two-tone, third-order intermodulation products. If two input RF signals are incident at the mixer RF port, they cause the mixer to generate the following two-tone intermodulation products.
![]()
where m1, m2, n = 0, 1, 2, 3,..., m and n are integers and can assume any value. Two-tone, third-order intermodulation products have the following frequencies:
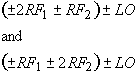
They are called third-order products because the coefficients of RF1 and RF2 sum to equal 3. Notice that the order of intermodulation products refers only to coefficients of the RF inputs and ddoes not include that of the LO. The order of the intermodulation product is important because a 1-dB change in the power level of each input RF signal causes the power level of each intermodulation procut to change by an amount of dB equal to its order. A 1-dB change in power of each of the two input RF signals causes the power level of each tow-tone third-order product to change by 3 dB.
Input intercept point is normally associated with tow-tone, third-order intermodulation products because the third-order product is closest in frequency to the desired IF output product of any tow-tone intermodulation product. The even-order, two-tone intermodulation products that exit form double and single-balanced mixers are suppressed far more than the odd-order products, due to mixer balance. Odd order intermoduation products containing even order LO harmonics are suppressed in double, but not in single balanced mixers. Third-order two-tone products follow the (m1 + m2) dB of output power to 1-dB of input-power-rule much more closely than the other higher-order, two-tone intermodulation products. Thow-tone intermodulation products with orders greater than 7 are rarely a problem unless RF input power comes within a few dB of LO input power.
Intercept point in normally presented as shown in figure 8. Input power is plotted along the horizontal axis, and output power is plotted along the vertical axis. Two lines are plotted: one relating IF output power to RF input power, and another relating intermodulation output power to RF input power.
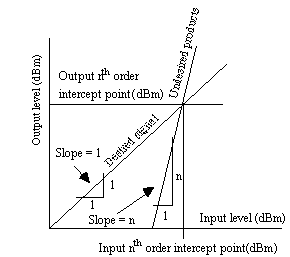
Figure 8. Intercept point definition
The point at which these lines intersect gives the input and output intercept points for the mixer at a particular set of input frequencies for a given LO power level and temperature.
A simple formula exists for calculating input intercept point, given teh level of intermodulatoin sujppression, the order of the intermodulation, and the input RF power levels giving rise to this level of suppression.
![]()
For example, if each input tone has -10 dBm of power, and the third-order, two-tone intermodulation suppression is 46 dBc, then the IIP is
![]()
Also, output and input intercept are related by the mixer conversion loss, or gain (for active mixers).
![]()
Voltage Standing Wave Ratio (VSWR) is the measure of mismatch offered to the system by the mixer, and is usually specified over a given bandwidth as a function of LO power and temperature. It is calculated as
![]()
where
![]()
![]() is the reflection coefficient,
is the reflection coefficient,
ZL is the input impedance of the mixer, and
Zo is the characteristic impedance of the system.
Since VSWR does not include the phase of the reflection coefficient, the system designer does not know if the input impedance is above or below the normal 50 Ω characteristic impedance. For example, if the LO port
VSWR is 2:1, measured in a 50 Ω system, the designer does not know if the LO port input impedance is 25 Ω or 100 Ω since both these impedances give a VSWR of 2:1. Actually, the input impedance of a broadband mixer swept over a frequency range of an octave, or more, usually rotates through the low and high impedances, roughly producing a circle centered at 50 Ω as vied on a Smith chart. Therefore, a given mixer having a LO VSWR of 2:1 over an octave bandwidth will have an input impedance varying from 25 Ω to 100 Ω, passing through an infinite number of complex impedance combinations as the LO frequency changes. The VSWR of the RF, LO, and IF ports are direct functions of the LO power, which establishes the operating point of the diodes in a diode ring mixer. Change in the LO power alters the diode operating point, resulting in a different impedance of all mixer ports, causing a corresponding change in VSWR. RF input power, which is usually much lower than LO input power, does not appreciably change the diode bias point and consequently, has little affect on VSWR. When the diode impedance changes, the input impedances of all three ports change. Hence, varying the LO power level will affect he VSWR of all three ports.
Joseph J. Carr, Mastering Radio Frequency Circuits Through Projects & Experiments, McGraw-Hill, 1994
The Watkins-Johnson Company, RF and Microwave Designer's Handbook, 1993