BARTLETT'S BISECTION THEOREM
Copyright 1999, Mike Ellis
| More Tutorials |
Bartlett's bisection theorem states that if a symmetrical network is bisected and one half is impedance-scaled including the termination, the response shape will not change. All odd-order Butterworth and odd-order Tchebyscheff filters satisfy this requirement, and also 3rd order inverse Tchebyscheff and 3rd order elliptic filters. The symmetry must include not only the topology but also the component values, therefore higher order inverse Tchebyscheff and elliptic filters are excluded. This extremely powerful result allows many passive filters to be modified for unequal source and load resistances.
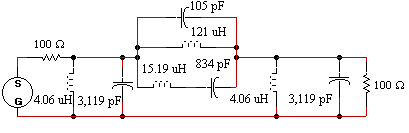
Example: Modify the circuit in figure 6.1 for a termination resistance of 1000 ohms.

Figure 1. Bandpass 3rd order elliptic filter with 1 dB passband ripple, 50 dB stopband attenuation, and a bandpass region of 1 MHz to 2 MHz.and load resistances.
In order to make the component values symetrical, the 105 pF capacitor is split into two series 210 pF capacitors. The 121 uH inductor is split into two series 60.5 uH inductors. The 15.19 uH inductor in series with the 834 pF capacitor is split into two 7.6 uH series inductors and two 1668 pF series capacitors. Those components on the right side of the dividing line in figure 2 are impedance scaled to increase their impedance by a factor of 10. The capacitor values therefore decrease by a factor of 10, and the inductor values are increased by a factor of 10.
Solution: The bisected circuit becomes
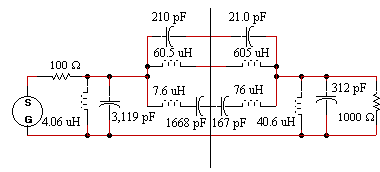
Figure 2. Bisected circuit.
Combining the series inductors and capacitors yields
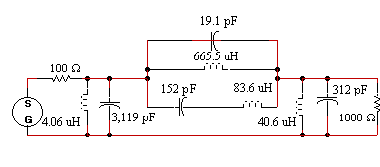
Figure 3. Final circuit after modification for a 100 ohm source impedance and 1000 ohm load impedance.
Bartlett's bisection theorem cannot be used to provide an impedance match between different source and load resistances but the transformed network will have the exact same response shape and phase as the original network.